(This is from a drawing session with a friend on Drawpile.)
When I struggle a bit with whatever's being taught in school, I approach harder stuff in my free time to maintain my dignity. It's a productive form of procrastination! I recently taught myself Lambert to solve equations with variable exponents and bases, and while I do feel better about myself, Lambert does not fully satisfy me.
Sometimes, it feels like people have such an insatiable need for solving problems that when they can't solve one, they'll make up something arbitrary so they can stop losing sleep over it. W-functions feel like one such case to me. When you solve a problem with a W-function, you still have to numerically approximate it, which you could've done from the start, so what's the point? We haven't solved the problem; we've just moved it!
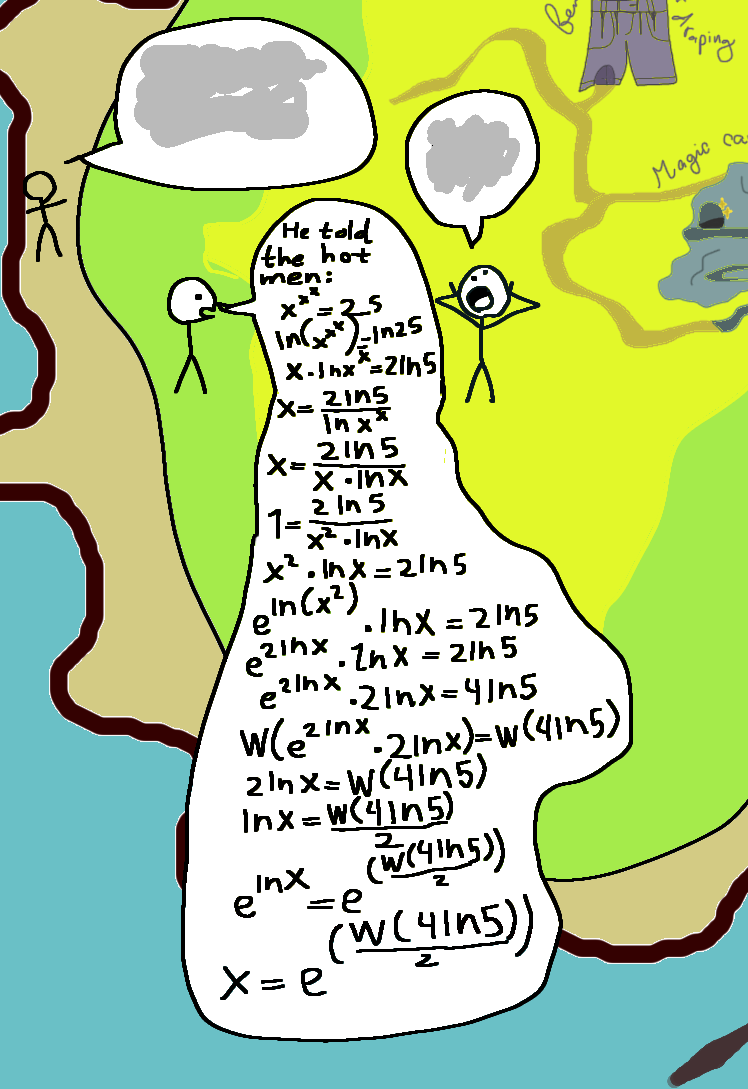
At the same though, I guess the the same abstraction applies to other inverse functions, such as roots and logarithms. As far as I know, there isn't a way to precisely calculate, let's say, the square root of seven numerically, but sqrt(7) expresses a number somewhere on the number line that we can't locate. However, Lambert doesn't feel as expressive to me. When you see something like x = sqrt(10), you can intuitively understand that we were trying to solve x^2 = 10, or when you see something like x = log(15), you can intuitively understand that we were trying to solve 10^x = 15, etc. But tell me, if you saw that x = e^(W(4ln5)/2) would you intuitively understand that we were trying to solve x^x^x = 25? Some might say that Lambert lets us notate the value of x in this case, but in my opinion, x^x^x = 25 expresses the value of x more clearly than e^(W(4ln5)/2).
To be fair to Lambert, it can be used to get exact numerical answers for some problems.
For example, you can use it to prove that x = 2 when x^x = 4.
x^x = 4
ln(x^x) = ln4
x * ln(x) = ln4
e^ln(x) * ln(x) = ln4
W(e^ln(x) * ln(x)) = W(ln4)
ln(x) = W(ln4)
ln(x) = W(ln(2^2))
ln(x) = W(2ln2)
ln(x) = W(e^ln2 * ln2)
ln(x) = ln2
e^ln(x) = e^ln2
x = 2
However, do you see the redundance here? In order to reformat ln4 into xe^x to unabstract the W-function, we had to know that 2^2 = 4 anyway, which we could've recognized from the start, so what did Lambert help us with here?
Let's take a look at another example: 3^x + x = 30.
3^x + x = 30
3^x = 30 - x
1 = (30 - x)3^-x
(30 - x)3^-x = 1
(30 - x)3^-x * 3^30 = 1 * 3^30
(30 - x)3^(30 - x) = 3^30
(30 - x)e^((ln3)(30 - x)) = 3^30
(ln3)(30 - x)e^((ln3)(30 - x)) = 3^30 * ln3
W((ln3)(30 - x)e^((ln3)(30 - x))) = W(3^30 * ln3)
(ln3)(30 - x) = W(3^30 * ln3)
Let's reformat the right hand side into xe^x so we can unabstract the W-function
3^30 * ln3
3^27 * 3^3 * ln3
3^3^3 * 3^3 * ln3
e^(ln(3^3^3)) * 3^3 * ln3
e^(ln(3^27)) * 27 * ln3
e^(27 * ln3) * 27 * ln3
Nice! So...
(ln3)(30 - x) = W(e^(27ln3) * 27ln3)
(ln3)(30 - x) = 27 * ln3
30 - x = 27
-x = -3
x = 3
If you're wondering if I found the solution myself, the answer is sadly no, but the solution definetely kicks ass!! Right?? My jaw dropped when I saw someone on YouTube solve it. When he was reformatting 3^30 * ln3 into xe^x, I felt like I was watching a zoo animal break out of its cage! It was nuts! However, even though that was an impressive display of mathematical knowledge, I still feel like Lambert has failed us here. Solving this problem with Lambert involves solving that reformatting subproblem, which (at least to me) requires a lot of experimentation and gut-feeling to figure out — experimentation that could've been applied to the original equation. Like, if you're clever enough to notice that 3^30 * ln3 can be rewritten as e^(27ln3) * 27ln3, you probably could've noticed that x was 3 initially with ease.
I get that Lambert allowed us to show our work in these examples. There would be an unexplained gap between the problem and the solution if we directly pointed out that x = 3 just because "we saw it", but it feels weird that some steps required us to take equal or even bigger unexplained leaps when solving it with Lambert.
These are still unfinished thoughts, though, and I'm far from a math expert! If you've been drafting a rebutal in your head while reading this, please send it my way! I would love to learn something!